CS 180 Project 3: Face Morphing and Modelling a Photo Collection

Overview

This project explores the realm of image morphing, specifically face morphing. To morph one image to another, we must first select correspondence points on both images that correspond to the same feature. Then by using the Delaunay traingulation algorithm, we can create a triangle mesh over our images, which we will use to perform our warping, as it is a change of basis between these triangles. Then, we can cross dissolve the pixel values of our warped images to create an intermediate image. These techniques were used to create a facial morphing animation, determine the mean face of a popluation, and extrapolate from the mean to create caricatures.

Defining Correspondences

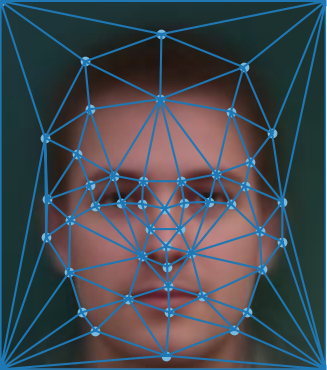
For this project, I decided to create a morphing animation from my face to my roommate Suchir's face. The first step in creating a facial morphing animation is to define correspondences between the two images. So I first cropped images of Suchir and me to be roughly the same size. Then using an online tool, I selected 53 correspondence points on our faces and additionally added the four corners of the image to create a total of 57 correspondences to perform the morphing. Then I performed the Delaunay triangluation algorithm on the average of the points selected in both images. The triangulation was performed on the average of the points to minimize the warping on the triangles.

suchir_tri_mesh — Suchir - Triangular Mesh

Computing the "Mid-Way Face"

To compute the "mid-way face" between Suchir and me, I warped both of our faces to the average geometry and then cross dissolved the pixel colors. The cross dissolving of pixel colors was quite straight-forward, simply computing $\frac{1}{2}$ (avg_im1 + avg_im2). However, the image warping was more involved. Given the triangular mesh created by the Delaunay triangulation, I computed a change of basis between triangles. The change of basis was computed in the following manner: $$p_{im1} = T_1T_2^{-1} (p_{im2} - og_2) + og_1$$ where $T_1$ is the transformation from a triangle in the original image to the standard basis, $T_2$ is the change of basis matrix from the corresponding triangle in the warped image to the standard basis, and $og_1$ and $og_2$ are the origins of the original and warped images, respectively. Note however, that $p_{im1}$ is not guaranteed to be a discrete pixel value. To account for this, I performed a linear interpolation with pixels neighboring $p_{im1}$, to determine the appropriate color value of pixel $p_{im2}$.

teja_suchir_midway — Teja-Suchir Midway Face

teja_mean — Teja Warped to Average Geometry

suchir_mean — Suchir Warped to Average Geometry

The Morph Sequence

Using the techinque explained above, I created a morphing animation from my to Suchir's face with a total of 45 frames. The geometry used was computed by a weighted average of the correspondence points of the original images. For frame i: ((num_frames - 1 - i) * im1_pts + i * im2_pts) / (num_frames - 1). The frames were then put together into a gif that runs at 30 fps.

The "Mean Face" of a Population

Here, I computed the average face of Danes, using the Danes dataset which consists of 37 images. In the dataset, .asf files were provided that contained the correspondence points for each of the images. The points were given as a fraction of the images width/height, so I had to scale them accordingly. So after scaling down each Dane image (to increase efficiency), I scaled the data points accordingly and computed the mean across the 37 images. Then similar to what I did previously with my and Suchir's face, I warped each of the images to the average geometry and cross dissolved the images to produce the average Danish face.

Additionally, I warped my face to the facial geometry average Dane and warped the average Dane to the geometry of my face. Here, I manually selected new correspondences for my image and the average Dane due to the need to resize and crop both images for alignment.

Caricatures - Extrapolating from the Mean

I also created caricatures of my face by extrapolating from the mean geometry between the average Dane and me. In order to do this, I performed a weighted average of the two images' correspondence points where one of the weights was a negative value, and the other was greater than 2. In a general form, the weighted average was computed by the following: new_pts = (α * teja_pts + β * avg_dane_pts)/2, where α < 0, β > 2, and α + β = 2. After computing these points, I simply warped my face to the new geometry.

Bells and Whistles: Changing Ethnicity

Here, I attempted to change my ethnicity by using an image of the average English male that I found online as a basis. First, I rescaled and aligned both images, and then defined correspondences as done previously. I tried a couple of things out when doing this. I first just warped my face to the geometry of the average Englishman. Then, I cross dissolved this with the original average English male image, using the general formula combined_img = (α * warped_teja + β * avg_englishman)/2, where α, β > 0, and α + β = 1. Additionally, I tried warping the average Englishman to my face's geometry and similarly played around with the cross dissolving ratios with the general formula combined_img = (γ * warped_teja + δ * avg_englishman)/2, where γ, δ > 0, and γ + δ = 1. The idea behind this was to see how changing my ethnicity would perform by only using geometry, only using the appearance (color), and a combination of both.

Teja Warped to Average Englishman	Cross Dissolve 1: α = 0.85, β = 1.15	Cross Dissolve 1: α = 0.65, β = 1.35
Average Englishman Warped to Teja	Cross Dissolve 1: γ = 0.85, δ = 1.15	Cross Dissolve 2: γ = 0.55, δ = 1.45

Original	Warped	Original	Warped
Original	Warped	Original	Warped